الرياضيات[1] علم مواضيعه مفاهيم مجردة والاصطلاحات الرياضية تدل على الكم، والعدد يدلّ على كمية المعدود والمقدار قابل للزيادة أو النقصان
الرياضيات[1] علم مواضيعه مفاهيم مجردة والاصطلاحات الرياضية تدل على الكم، والعدد يدلّ على كمية المعدود والمقدار قابل للزيادة أو النقصان وعندما نستطيع قياس المقدار نطلق عليه اسم الكم. لذلك عرف بعض العلماء الرياضيات بأنه علم القياس. تعتبر الرياضيات لغة العلوم إذ إن هذه العلوم لا تكتمل إلا عندما نحول نتائجها إلى معادلات ونحول ثوابتها إلى خطوط بيانية.
تعرف الرياضيات بأنها دراسة القياس والحساب والهندسة. هذا بالإضافة إلى المفاهيم الحديثة نسبياً ومنها البنية، الفضاء أو الفراغ، والتغير والأبعاد. وبشكل عام قد يعرفها البعض على أنها دراسة البنى المجردة باستخدام المنطق والبراهين الرياضية والتدوين الرياضي. وبشكل أكثر عمومية، قد تعرف الرياضيات أيضاً على أنها دراسة الأعداد وأنماطها.
ولقد نشأت الرياضيات عند قيام الإنسان بقياس ما يشاهده من ظواهر الطبيعة وبناء على فطرة وخاصية في الإنسان ألا وهي اهتمامه بقياس كل ما حوله إلى جانب احتياجاته العملية فهكذا كان هناك ضرورة لقياس قسمة الأقوات (الطعام) بين أفراد العائلة وقياس الوقت والفصول والمحاصيل الزراعيةوتقسيم الأراضي وغنائم الحملات الحربية والمحاسبة للتمكن من الإتجار إلى جانب علم الملاحة بالاهتداء بالنجوم في السفر والترحال للتجارة والسياحة والقياسات اللازمة لتشييد الأبنية والمدن.
وهكذا فإن البنى الرياضية التي يدرسها الرياضيون غالباً ما يعود أصلها إلى العلوم الطبيعية، وخاصة علم الطبيعة، ولكن الرياضيين يقومون بتعريف ودراسة بنى أخرى لأغراض رياضية بحتة، لأن هذه البنى قد توفر تعميما لحقول أخرى من الرياضيات مثلاً، أو أن تكون عاملاً مساعدا في حسابات معينة، وأخيراً فإن الرياضيين قد يدرسون حقولا معينة من الرياضيات لتحمسهم لها، معتبرين أن الرياضيات هي فن وليس علماً تطبيقيا.
ولعلم الرياضيات دور بارز في علوم المادّة (أي الفيزياء والكيمياء) وعلم الأحياء (البيولوجيا)، فضلاً عن دوره المتميز في العلوم الإنسانية جمعاء.
محتويات
[أخف]التاريخ[عدل]
 مقالة مفصلة: تاريخ الرياضيات
مقالة مفصلة: تاريخ الرياضيات
كان الكُتاب البابليون منذ أكثر من 3000 عام يمارسون كتابة الأعداد وحساب الفوائد ولا سيما في الأعمال التجارية ببابل. وكانت الأعداد والعمليات الحسابية تدون فوق ألواح الصلصال بقلم من البوص المدبب. ثم توضع في الفرن لتجف. وكانوا يعرفون الجمع والضرب والطرح والقسمة. ولم يكونوا يستخدمون فيها النظام العشري المتبع حاليا مما زادها صعوبة حيث كانوا يتبعون النظام الستيني الذي يتكون من 60 رمزا للدلالة على الأعداد من 1-60. وطور قدماء المصريين هذا النظام في مسح الأراضي بعد كل فيضان لتقدير الضرائب. كما كانوا يتبعون النظام العشري وهو العد بالآحاد والعشرات والمئات. لكنهم لم يعرفوا الصفر. لهذا كانوا يكتبون 600 بوضع 6 رموز يعبر كل رمز على 100.
الرياضيات في علوم المادة[عدل]
يبقى علم الفيزياء علما استقرائياً يعتمد في الأساس على مراقبة الظواهر الطبيعية واختبارها، ويستطيع في أقصى حده التعبير عن القوانين بلغة رياضية، فتكون الرياضيات في مجال علوم المادة لغة تعبير أكثر منها منهج اكتشاف، وهناك حالات عديدة كانت الرياضيات فيها أسلوب اكتشاف وبرهنة. فقد اكتشف الفلكي الفرنسي أوربان لوفيريي بالحسابات الرياضية مكان كوكب نبتون وبعده وكتلته قبل التحقق من وجوده الفعلي بالرصد وكان الفكر الرياضي عند "نيوتن" و"أينشتاين" سابقا إلى حد كبير على الاختبار، لكن يبقى الاختبار الضامن الأخير لصحة الاكتشافات في علوم المادة. أما فرضية تحويل الكون برمته إلى معادلة رياضية كبرى فيبقى حلماَ راود أذهان الفلاسفة والعلماء أمثال "ديكارت"، ولكن هذا الهدف الكبير يبقى مجرّد فرضيّة دونها صعوبات وتجاذبات علمية وفلسفية، فالعالم لا يستطيع استعمال المنهج الرياضي الاستنباطي في سائر العلوم إلا إذا سلب الواقع كثيرا من مضمونه.
فاللغة الرياضية توفر للقوانين العلمية مزيدا من الدقة، ومن أبرز الأمثلة على دور الرياضيات في علوم المادة: قياس سرعة الرياح، وقياس قوة الزلازل، وقياس الضغط الجوي.
الرياضيات في علوم الأحياء[عدل]
إن نجاح المنهج الاختباري في علوم الأحياء هيأها لاستعمال اللغة الرياضية الرائجة جدا في مجال العلوم الفيزيوكيميائية. ولقد عارض بعض العلماء هذا داعين إلى الحذر وعدم إقحام الرياضيات في علوم الأحياء قبل أن تمر هذه الأخيرة بشكل واف على مشرحة التحليل. فالعلم الذي يبلغ مبلغا كافيا من التطور هو الذي يمكن أن يطمح إلى هذه الدرجة العلمية الرياضية.
وكان علم الوراثة الأول من علوم الأحياء الذي اتبع علوم المادة في مسارها الرياضي، وقد طبقت قوانين "مندل" في المجال الحيواني بقصد تأصيل بعض الحيوانات وعزل خصائص معينة كاللون والشكل والقد. وركز العالم "مورغان" اختياراته على ذبابة الدروزوفيل فتوصل إلى تحديد الجينات الوراثية في كروموسومات نواة الخلية.
إن علماء البيولوجيا يعتبرون الإحصاءات الرياضية بمثابة استقصاء وشرح متميز للمعطيات الطبية. فإن قياس الثوابت البيولوجية والتسجيلات البيانية تشكل لغة شائعة جدا في علوم الأحياء. فتخطيط الدماغ، وتخطيط القلب، وقياس نسبة الزلال، وقياس نسبة السكر في الدم، وإحصاء عدد كريات الدم الحمراء والبيضاء، وقياس النمو والوزن كلها دلائل على دخول الرياضيات في علوم الأحياء.
الرياضيات في العلوم الإنسانية[عدل]
تضم العلوم الإنسانية علم الاقتصاد والاجتماع والتاريخ والنفس والأخلاق وما سواها. فالمجتمعات الصناعية تعتمد على اللغة الرياضية من أجل تطوير الواقع الذي تعيش فيه، فالاقتصاد يقوم على التخطيط الذي يعد أسلوبا للسيطرة على اقتصاد البلد ومحوره الأساسي الرياضيات. كذلك علم الاجتماع الذي يرتكز على الاستبيان والجداول الإحصائية والخطوط البيانية أثناء دراسة لحالة فقر أو نسبة الهجرة السكانية إلى الخارج أو نسبة البطالة. أما بالنسبة للتاريخ، فالرياضيات تجعل عملية التأريخ أكثر موضوعية ودقة من خلال تحديد الفترة الزمنية لحادثة ما وتدوين نتائجها على مختلف الصعد. وتستخدم اللغة الرقمية في العديد من الدراسات لعلم النفس خاصة عندى قياس الفروقات الفردية ونسبة الذكاء. غير أن الرياضيات لا تستطيع الدخول على علم الأخلاق بسبب الموضوعات التي يحويها كالإرادة والضمير والحرية والمسؤولية والحق والواجب، فهي بالأمور المعنوية التي لا يصح معها استعمال القياس أو الكم.
مجالات الرياضيات[عدل]
أدى الانتشار الواسع للمعرفة في العصر العلمي إلى التخصص حيث يوجد حاليا ما لا يقل عن المئات من التخصصات في الرياضيات، إذ يحتل تصنيف مواضيع الرياضيات ستا وأربعين صفحة.
أسس وفلسفة الرياضيات[عدل]
بصفة عامة، يمكن للرياضيات أن يقسم إلى دراسة الكمية والبنية والفضاء والتغير (مما يعني الحسابيات والجبر والهندسة والتحليل).
الرياضيات البحتة[عدل]
قد تقسم الرياضيات إلى فروع حسب موضوع الدراسة الأساسي.
الكمية[عدل]
 |  |  | |
| أعداد طبيعية | أعداد صحيحة | أعداد كسرية | |
 |  | ||
| أعداد حقيقية | أعداد مركبة أو عقدية |
- عدد – عدد طبيعي – عدد صحيح – عدد كسري – عدد حقيقي – عدد عقدي – عدد فوق عقدي – كواتيرنيون – اوكتونيون – سيدينيون – عدد فوق حقيقي – عدد حقيقي فائق – عدد ترتيبي – عدد كمي – عدد بي – متوالية صحيحة – ثابت رياضي – أسماء الأعداد – اللانهاية – الأساس (رياضيات)
البنية[عدل]
انظر إلى بنية رياضية.
جبر تجريدي – نظرية الأعداد – هندسة جبرية – نظرية المجموعات – مونويد – التحليل الرياضي – الطوبولوجيا – الجبر الخطي – نظرية المخططات – الجبر الشامل – نظرية الزمر – نظرية الترتيب – نظرية القياس
الفضاء[عدل]
قد يسمى الفضاء أيضا فراغا.
التغير[عدل]
 |  |  |  |  |  |
| تفاضل وتكامل | تفاضل شعاعي | معادلة تفاضلية | نظام تحريكي | نظرية الشواش | تحليل مركب |
الرياضيات التطبيقية[عدل]
تدرس الرياضيات التطبيقية الطرق والوسائل الرياضية التي تستعمل في مجالات أخرى كالهندسة والعلوم والأعمال والصناعة والتجارة. وترتبط الرياضيات التطبيقية ارتباطا كبيرا بالرياضيات البحتة.
قد تضم الرياضيات التطبيقية مجالات الميكانيك والتحليل العددي والاستمثال الرياضي والرياضيات الاقتصادية ونظرية الألعاب والبيولوجيا الرياضية وعلم التعمية ونظرية المعلومات وميكانيك السوائل.
الإحصاء وعلوم أخرى مساعدة على اتخاد القرارات[عدل]
للرياضيات التطبيقية تداخل مع تخصص الإحصاء حيث تعتمد نظرياته على الرياضيات وخصوصا نظرية الاحتمال.
الرياضيات الحسابية[عدل]
تدرس الرياضيات الحسابية (بالإنجليزي: Computational mathematics) طرق حلحلة المعضلات الرياضية التي تتطلب قدرات حسابية تفوق القدرة الإنسانية، والتحليل العددي يأتي في هذا الاتجاه أيضا.
 |  |  |  |  | ||
| فيزياء رياضية | جريان الموائع | تحليل عددي | الاستمثال | نظرية الاحتمال | إحصاء | علم التعمية |
 |  |  | 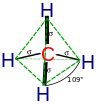 | |||
| رياضيات مالية | نظرية الألعاب | علم الأحياء الرياضي | كيمياء رياضية | الاقتصاد الرياضي | نظرية التحكم |
تعليم[عدل]
يتم تدريس الرياضيات بطرق مختلفة في الجامعات حول العالم. في قارتي أمريكا يدرس طلاب الهندسة والرياضيات حساب التفاضل والتكامل(Calculus) لمدة ثلاث فصول دراسية (سنة ونصف). خلال هذه الفترة يتعلم الطلاب العديد من المهارات والخبرات الهامة مثل كيفية اشتقاق ومكاملة المعادلات التي تحوي مجهول واحد أو أكثر وكيفية ضرب وجمع الأشعة في مستوي ثلاثي الأبعاد. بعد اجتياز هذا الصف بنجاح، يبدأ الطلاب بدراسة الجبر الخطي (Linear Algebra). يمكن أن يأخذ الطلاب المزيد من صفوف الرياضيات قبل التخرج وذلك يعتمد على مجال دراستهم.[2][3]
هل الرياضيات مهنة ؟[عدل]
انظر إلى وسام فيلدز وجائزة وولف في الرياضيات وجائزة آبل.
هل الرياضيات علم ؟[عدل]
انظر أيضا تعريف الرياضيات.
وصف كارل فريدريش غاوس الرياضيات بأنها ملكة العلوم.
وصف كارل فريدريش غاوس الرياضيات بأنها ملكة العلوم.
يعتقد عدد من الفلاسفة أنه من غير الممكن تخطيئ الرياضيات تجريبيا، وبالتالي، فهي ليست بعلم إذا ما نُظر إلى تعريف كارل بوبر للعلم[5]. ولكن في ثلاثينات القرن العشرين، جاءت مبرهنات عدم الاكتمال لغودل لكي تقنع العديد من علماء الرياضيات بأنه لا يمكن اختزال الرياضيات في المنطق وحده. مما دفع بكارل بوبر إلى الاستنتاج أن أعظم النظريات الرياضية هي، كما هو الحال في الفيزياء والبيولوجيا، فرضية ثم استنتاج استنباطي.
تقسيم أولى لفروع الرياضيات[عدل]
من الرياضيات البحتة
- من فروع المنطق:
- المنطق التجريدي.
- الجبر المنطقي أو الجبر البولياني وينبع منه
- حساب القضايا.
- منطق الرتبة الأولى يحتوى هذا الفرع على القواعد والأصول اللازمة لصياغة نظريات الذكاء الاصطناعي وهو يعتمد بدوره على مبادئ الجبر البولياني ومنطق القضايا.
- المنطق الوقتي.
- المنطق الضبابي.
- نظرية الاعتقاد.
- المنطق القافي.
- من فروع الرياضيات المتقطعة:
- اللغات الشكلية ونظرية الآليات
- نظرية المخططات وهي دراسة نظم ذات بنية شبكية وتتضمن على دراسة الشبكات وعبور المخططات والشجر وأطياف المخططات وغير ذلك.
- نظرية المجموعات المبسطة.
- نظرية الأعداد.
- من فروع الجبر:
- جبر الأعداد الحقيقية (الجبر والمقابلة للخوارزمي).
- الجبر التجريدي (يشتمل على القواعد المنطقية لحساب مختلف مجموعات الأعداد مثل حساب الأعداد الحقيقية والمركبة إلخ)
- نظرية الزمر.
- حساب المجموعات (الفئات).
- حساب المتتاليات.
- حساب المتجهات.
- الجبر الخطي.
- حساب المصفوفات.
- الجبر البولياني
- ما وراء الرياضيات: ويشتمل ذلك على سبيل المثال على نظرية جودل وبحوث هيلبرت وبرتراند راسل حول تعريف وتبويب بنية الرياضات بأجمعها.
- من فروع الهندسة:
- الهندسة الإقليدية.
- الهندسة الفراغية.
- الهندسة الإسقاطية.
- حساب المثلثات.
- الهندسة التحليلية.
- الهندسة الجبرية.
- الهندسة التفاضلية.
- الهندسة التضاريسية.
- الهندسة التضاريسية لمجاميع النقاط.
- الهندسة التضاريسية الجبرية.
- نظرية العقد.
- من فروع التحليل:
- الحساب المتناهي (حساب التفاضل والتكامل).
- المعادلات التفاضلية والمعادلات التكاملية.
- تحليل الأعداد الحقيقية.
- التحليل العددي.
- التحليل التوافقي.
- التحليل الدالي.
- نظرية الدالات أو تحليل الدالات المركبة.
- التحليل اللا-قياسي.
- نظرية القياس.
- نظرية الألعاب ولها تطبيقات في الاقتصاد وعلوم الإدارة والتخطيط.
- علم الاحتمالات والإحصائيات.
- علم النظم
- نظرية الشواش والنظم اللا-خطية.
- نظرية التحكم الآلي.
- علوم الحاسبات الآلية:
- نظرية الحوسبة.
- تحليل الخوارزميات.
- الذكاء الاصطناعي.
- التعلم الآلى ويشتمل على
- نظريات التعلم التوأصلي والشبكات العصبية أو العصبونية.
- نظريات التعلم التطورى: البرمجة والخوارزميات الوراثية والتطورية.
- الإثبات الآلى للنظريات.
- البحث المتوالى والمتوازي وفوز المباريات.
- التعلم الآلى ويشتمل على
- تصميم الدارات المنطقية.
- علم المعلومات أو العلوم المعلوماتية.
- علم إدارة نظم المعلومات.
- علوم البرمجيات.
- الاستمثال تعرف فروع هذا القسم بالبرمجة للإشارة إلى أن المراد هي إيجاد أدنى حلول للمعادلات تحت التحليل مثلا تحليل سيمبلكس.
- البرمجة الخطية.
- البرمجة الكاملة.
- البرمجة المتحركة.
- بحوث العمليات.
- علوم الطبيعة الرياضياتية: وتشمل على فروع العلوم والنظريات الطبيعية التي تعتمد بالأساس في صياغتها على التحليل والبرهنة الرياضية أكثر من قياس التجارب والظواهر الطبيعية ومنها
- نظرية الكم أو النظرية الكمومية أو علم الحركيات الكمية.
- الميكانيكا أو الحركيات الإحصائية.
- ومنها أيضا دراسة حلول الدالات المجهولة في التصميم الهندسي والصناعي والتي تعتمد على حساب المعادلات التفاضلية التي تصف النظم تحت التصميم.
- ميكانيكا هاملتون.
- التحليل العددي.
- علم الشفرات.
الرياضيات المتقطعة[عدل]
| نظرية المجموعات المبسطة | نظرية الحوسبة |
| علم التعمية | نظرية المخططات |
المبرهنات والحدسيات الهامة[عدل]
- مبرهنة فيثاغورث – مبرهنة طاليس –مبرهنة الكاشي –مبرهنة فيرما الأخيرة – حدسية غولدباخ – حدسية التوأمين الأولية – مبرهنة عدم الاكتمال لغودل – حدسية بوانكاريه – قطر كانتور – مبرهنة الألوان الأربعة – قضية زورن المساعدة – هوية اويلر – أطروحة تشرش-تورينغ
- فرضية ريمان – فرضية الاستمرارية – P=NP – مبرهنة الحد المركزية – المبرهنة الأساسية في التكامل – المبرهنة الأساسية في الجبر – المبرهنة الأساسية في الحساب – المبرهنة الأساسية في الهندسة الإسقاطية – مبرهنات تصنيف السطوح – مبرهنة غاوس-بونيت
رسم الأشكال الرياضية[عدل]
يمكن رسم الأشكال الرياضية الثلاثية الأبعاد المعقدة بواسطة برنامج خاص يدعى ماتلاب(Matlab). يجب كتابة المعادلة الرياضية للشكل في مربع خاص حتى يقوم البرنامج برسمه. هذا البرنامج يسمح للمستخدم بتدوير الشكل حول إحدى محاوره الثلاث ليتمكن المستخدم من رؤية الشكل من كافة النواحي. أيضا يسمح للمستخدم بتغيير لون وحجم الشكل المرسوم ليتوافق مع رغبة واحتياجات المستخدم[6]. هذا البرنامج أيضا يستخدم في رسم الأشكال الثنائية الأبعاد.يقوم علماء البيولوجيا احيانا باستخدام هذا البرنامح احيانا لرسم الحمض النووي الريبوزي(DNA) التي غالبا ما يكون لها أشكال معقدة ومتداخلة.
بعض أعلام الرياضيات[عدل]
من أهم مطوري الرياضيات القديمة والحديثة نجد:
رياضياتية (بالإنجليزية: mathematical) صفة كل ما يتعلق بعلم رياضيات من أشكال ورمز وصيغ ومشكلات. فإذا كان رياضيات هو المتخصص في رياضيات، فإن مجال دراسته وبحثه يتعلق بمجموعة من الرموز والصيغ والأشكال والإجراءات التي تُسمى رياضياتية لانتسابها إلى رياضيات ولتمييزها عن الأمور رياضة التي تتعلق بالرياضةكممارسة قائمة على توظيف وتمرين وتشغيل الجسم البشري.
انظر أيضاً[عدل]
 مقالة مفصلة: قائمة مواضيع الرياضيات
مقالة مفصلة: قائمة مواضيع الرياضيات
- القلق الرياضياتي,
- تعليم الرياضيات,
- أنظمة العدّ,
- مهارات ما قبل تعلم الرياضيات
- الرياضيات في الفيزياء.
- مكافحة العنصرية في تدريس الرياضيات
مراجع[عدل]
- ^ (باليونانية: μαθηματικός) وترجمها كل من ابن رشد وأُسطات إلى كلمتي التعاليمية والتعليمية
- ^ http://www.ccny.cuny.edu/registrar/upload/Computer-Science-2011-2012-20120502.pdf
- ^ Anthropology
- ^ Zeidler، Eberhard (2004). Oxford User's Guide to Mathematics. Oxford, UK: Oxford University Press. صفحة 1188. ISBN 0-19-850763-1.
- ^ Shasha, Dennis Elliot; Lazere, Cathy A. (1998). Out of Their Minds: The Lives and Discoveries of 15 Great Computer Scientists. Springer. صفحة 228.
- ^ Getting Started with MATLAB
وصلات خارجية[عدل]
- Free Mathematics books Free Mathematics books collection.
- Encyclopaedia of Mathematics online encyclopaedia from Springer, Graduate-level reference work with over 8,000 entries, illuminating nearly 50,000 notions in mathematics.
- HyperMath site at Georgia State University
- FreeScience Library The mathematics section of FreeScience library
- Rusin, Dave: The Mathematical Atlas. A guided tour through the various branches of modern mathematics. (Can also be found at NIU.edu.)